Signals and Systems Chapter 1 Problems Part 3 (1.32-1.47)

1 Problem 1.32

Problem 1.32a

Let \(T\) be the fundamental period of \(x(t)\), then we have \(x(t+T) = x(t)\). So \( y_{1}(t) = x(2t) = x(2t + T) = x(2(t+ \frac{T}{2} ))= y_{1}(t+\frac{T}{2})\), \(y_{1}(t)\) is periodic and the fundamental period is \( \frac{T}{2} \) which is consistent with our commonsense that \(y_{1}(t)\) is an speeded up version of \(x(t)\).

Problem 1.32b

Let \(T\) be the fundamental period of \(y_{1}(t)\), then based on the analysis of Problem 1.32a , we have \(x(t)\) is a slowed down version of \(y_{1}(t)\), hense \(x(t)\) is periodic and has fundamental period \(2T\).

Problem 1.32c

Let \(T\) be the fundamental period of \(x(t)\), then we have \(x(t+T) = x(t)\). So \( y_{2}(t) = x(\tfrac{t}{2}) = x(\tfrac{t}{2} + T) = x(\frac{t+ 2T}{2})= y_{2}(t+2T)\), \(y_{2}(t)\) is periodic and the fundamental period is \(2T \) which is consistent with our commonsense that \(y_{2}(t)\) is an slowed down version of \(x(t)\).

Problem 1.32d

Let \(T\) be the fundamental period of \(y_{2}(t)\), then based on the analysis of Problem 1.32c , we have \(x(t)\) is a speeded up version of \(y_{2}(t)\), hense \(x(t)\) is periodic and has fundamental period \(\frac{T}{2}\).

2 Problem 1.33

Problem 1.33a

Let \(N\) be the fundamental period of \(x[n]\), then \(x[n+N] = x[n]\), and \(y_{1}[n] = x[2n] = x[2n+N] = y_{1}[n+ \frac{N}{2}]\). If \(N\) is even, then \(y_{1}[n]\) has fundamental period \(\frac{N}{2}\). It is a little tricky that when \(N\) is odd \(\frac{N}{2}\) has no meaning. If \(N\) is odd, we have to express \(y_{1}[n] = x[2n] = x[2n+2N] = y_{1}[n+ N]\) hence \(y_{1}[n]\) has fundamental period \(N\) if \(N\) is odd.

Problem 1.33b

We can see \(y_{1}[n]\) is not only a speeded up version but also a down sampling version of \(x[n]\). we cannot determine whether or not \(y_{1}[n]\) is periodic based on that \(x[n]\) is periodic. We can only tell that the even indexed value of \(x[n]\) is period. we know nothing about the odd indexed value of \(x[n]\). An example is given below:

The given \(x[n]\) is periodic at \(2n\) but is random at \(2n+1\).

Problem 1.33c

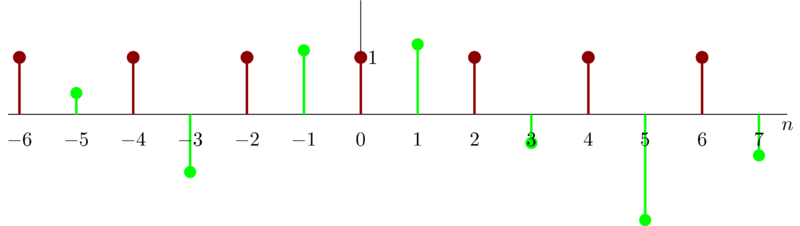
\(y_{2}[n]\) can treated as interpolation of \(x[n]\) with zero. So \(y_{2}[n]\) is periodic with fundamental period \(2N\) where \(N\) is fundamental period of \(x[n]\).

Problem 1.33d

Based on analysis of Problem 1.33c , \(y_{2}[n]\) has fundamental period \(2N\) where \(N\) is the fundamental period of \(x[n]\).

Based on the fact that only integer is valid for the independent variable of discrete-time signal, \(y_{2}[n]\) contains all the value of \(x[n]\) at the even index whereas at the odd index \(y_{2}[n]= 0\).

3 Problem 1.34

Problem 1.34a

If \(x[n]\) is an odd signal, then we have \(x[n] = -x[-n]\) and \(x[0]=0 \), so

\begin{eqnarray*} \sum_{n=-\infty}^{+\infty} x[n] &=& \sum_{n=0}^{+\infty} x[n] + \sum_{-\infty}^{0} x[n] \\
&=& \sum_{n=0}^{\infty} \big( x[n] + x[-n] \big) \\
&=& 0 \end{eqnarray*}

Problem 1.34b

Because \(x_{1}[n]\) is an odd signal, \(x_{1}[n] = -x_{1}[-n]\). Because \(x_{2}[n]\) is an even signal, \(x_{2}[n] = x_{2}[-n]\). we have

\begin{equation*} x_{1}[n]x_{2}[n] = -x_{1}[-n]x_{2}[-n] \\
\end{equation*}

i.e. \(x_{1}[n]x_{2}[n]\) is an odd signal.

Problem 1.34c

\begin{eqnarray*} x_{e}[n] &=& \frac{x[n] + x[-n]}{2} \\
x_{o}[n] &=& \frac{x[n] - x[-n]}{2} \end{eqnarray*}

Then we have

\begin{eqnarray*} \sum_{n=-\infty}^{+\infty} x_{e}^{2}[n] &=& \sum_{n=-\infty}^{+\infty} \bigg( \frac{ x[n] + x[-n] }{2} \bigg)^{4} \\
&=& \sum_{n=-\infty}^{+\infty} \bigg( \frac{ x^{2}[n] + x^{2}[-n] + 2x[n]x[-n]}{2} \bigg) \end{eqnarray*}

\begin{eqnarray*} \sum_{n=-\infty}^{+\infty} x_{o}^{2}[n] &=& \sum_{n=-\infty}^{+\infty} \bigg( \frac{ x[n] - x[-n] }{2} \bigg)^{2} \\
&=& \sum_{n=-\infty}^{+\infty} \bigg( \frac{ x^{2}[n] + x^{2}[-n] - 2x[n]x[-n]}{4} \bigg) \end{eqnarray*}

Then we add the above two equations and get

\begin{eqnarray*} \sum_{n=-\infty}^{+\infty} x_{e}^{2}[n] + \sum_{n=-\infty}^{+\infty} x_{o}^{2}[n] &=& \sum_{n=-\infty}^{+\infty} \frac{x^{2}[n] + x^{2}[-n]}{2} \\
&=& \sum_{n=-\infty}^{+\infty} x^{2}[n] \end{eqnarray*}

This conclusion tells us that even we seperate the signal into two parts(even part and odd part), the sum of energy from the even part and odd part is the total energy of the original signal.

Let

\begin{eqnarray*} \int_{-\infty}^{+\infty} x^{2}(t) dt &=& \int_{-\infty}^{+\infty} ( x_{e}(t) + x_{o}(t) )^{2}dt \\
&=& \int_{-\infty}^{+\infty} x_{e}^{2}(t)dt + \int_{-\infty}^{+\infty} x_{o}^{2}(t) dt + \int_{-\infty}^{+\infty} x_{e}(t)x_{o}(t) dt \\
&=& \int_{-\infty}^{+\infty} x_{e}^{2}(t)dt + \int_{-\infty}^{+\infty} x_{o}^{2}(t) dt \end{eqnarray*}

Notice that \(x_{e}(t)x_{o}(t)\) is and odd signal, so \( \int_{-\infty}^{+\infty} x_{e}(t)x_{o}(t) dt = 0 \)

4 Problem 1.35

5 Problem 1.36

Problem 1.36a

Problem 1.36b

Based on the analysis of Problem 1.36a, we have fundamental period of \(x[n]\)

\begin{equation*} N = m\frac{T_{0}}{T} = m \frac{q}{p} \end{equation*}

Where \(m\) is the minimum integer so that \(N\) is an integer. Based on the conclusion of Problem 1.35 , we can re-express \(N\) as

\begin{equation*} N = \frac{q}{\mathrm{gcd}(p,q)} \end{equation*}

Where \(m = \frac{p}{\mathrm{gcd}(p,q)}\). The fundamental frequency is

\begin{equation*} \frac{2\pi}{N} = \frac{2\pi \mathrm{gcd}(p,q)}{q} = \omega_{0}T_{0} \frac{\mathrm{gcd}(p,q)}{q} = \omega_{0}T\frac{\mathrm{gcd}(p,q)}{p} \end{equation*}

Problem 1.36c

The fundamental period of \(x(t)\) is \(T_{0} = \frac{2\pi}{\omega_{0}}\) and \(x[n]\) , \(N= \frac{q}{\mathrm{gcd}(p,q)}\). we have

\begin{equation*} \frac{N}{T_{0}}= \frac{Np}{Tq} = \frac{q}{\mathrm{gcd}(p,q)T} \frac{p}{q} = \frac{p}{\mathrm{gcd}(p,q)T} \end{equation*}

So, the discrete-time version of signal \(x(t)\) need at least \(\frac{p}{\mathrm{gcd}(p,q)T}\) periods of \(x(t)\) to obtain one period of \(x[n]\).

Let’s talk more about this problem. This problem preliminary discloses the concept of sampling which is a main method of obtaining discrete-time signal from continuous-time signal. Now let’s put Nyquist’s sampling theory aside and focus on the sampling itself.

Suppose we have a continuous-time signal

\begin{equation*} x(t) = \cos(4\pi t) \end{equation*}

whose fundamental period is \(T_{0} = \frac{2\pi }{4\pi} = \frac{1}{2}\). Then the sampling interval \(T\) must satisfies that \(T/T_{0}\) is a rational number so that \(x[n]= x(nT)= \cos(4\pi nT )\) is a periodic signal.

Let \(T\), say, be \( \frac{1}{5} \), then

\begin{equation*} \frac{T}{T_{0}} = \frac{2}{5} \end{equation*}

The fundamental period of \(x[n]\) is \( N = \frac{q}{\mathrm{gcd}(p,q)} = \frac{5}{\mathrm{gcd}(2,5)} = 5 \).

We can visualize \(x(t)\) and \(x[n]\) as below.

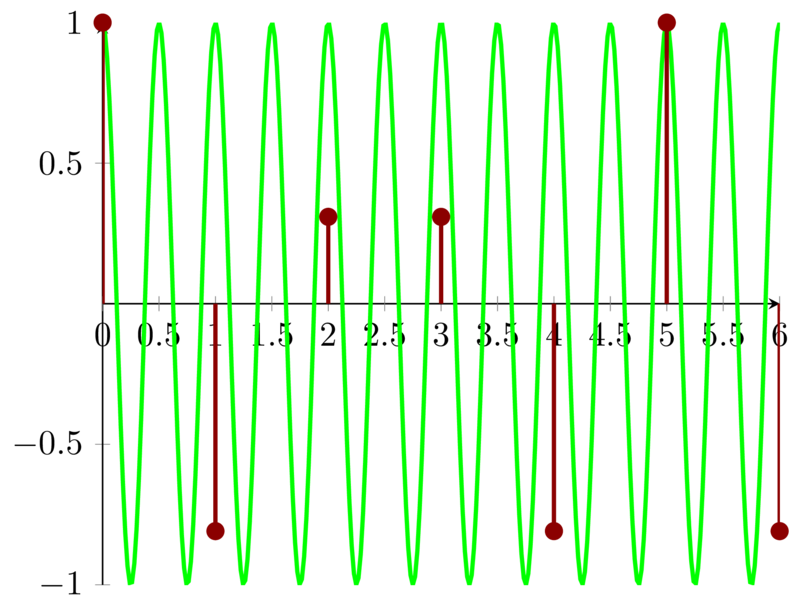
From the above figure, we can see that the discrete-time signal \(x[n]\) has fundamental period of \(5\) and its counterparts has fundamental period \(\frac{1}{2}\). We need at least \(10\) period of \(x(t)\) to get one period of \(x[n]\).

Now, if we take the Nyquist’s sampling into consideration, we must sampling a baseband signal with at least two times higher frequency of the signal to recover the baseband signal without alias. i.e. we must sample \(x(t) = \cos(4\pi t)\) with a signal of fundamental frequency \(8\pi\) to get signal \(x[n] = \cos(8\pi n)\).

6 Problem 1.37

Problem 1.37a

by the definition of correlation, we have

\begin{equation*} \phi_{yx} = \int_{-\infty}^{+\infty} y(t + \tau)x(\tau) d \tau \end{equation*}

we set \(t+ \tau = s\), then

\begin{eqnarray*} \phi_{yx}(t) &=& \int_{-\infty}^{+\infty} y(t + \tau)x(\tau) d \tau \\
&=& \int_{-\infty}^{+\infty} x(s-t) y(s) ds \\
&=& \phi_{xy}(-t) \end{eqnarray*}

Using the same procedure, we can also have \( \phi_{xy}(t) = \phi_{yx}(-t) \).

Problem 1.37b

we have

\begin{equation*} \phi_{xx}(t) = \int_{-\infty}^{+\infty} x(t+\tau)x(\tau) d\tau \end{equation*}

the odd part of \(\phi_{xx}(t)\) can be expressed as

\begin{equation*} \phi_{oxx}(t) = \frac{\phi_{xx}(t) - \phi_{xx}(-t)}{2} \end{equation*}

Based on Problem 1.37a, we have \( \phi_{xx}(t) = \phi_{xx}(-t) \) , so \(\phi_{oxx}(t) = 0\). which means that \(\phi_{oxx}(t)\) is an even signal.

Problem 1.37c

\begin{eqnarray*} \phi_{xy}(t) &=& \int_{-\infty}^{+\infty} x(t+ \tau) y(\tau)d\tau \\
&=& \int_{-\infty}^{+\infty} x(t+ \tau) x(\tau + T)d\tau \\
&=& \int_{-\infty}^{+\infty} x(t + s -T) x(s) ds \end{eqnarray*}

So we have \(\phi_{xy}(t) = \phi_{xx}(t-T)\).

\begin{eqnarray*} \phi_{yy}(t) &=& \int_{-\infty}^{+\infty} y(t+ \tau) y(\tau)d\tau \\
&=& \int_{-\infty}^{+\infty} x(t+ \tau + T) x(\tau + T)d\tau \\
&=& \int_{-\infty}^{+\infty} x(t + s) x(s) ds \end{eqnarray*}

So we have \(\phi_{yy}(t) = \phi_{xx}(t)\).

7 Problem 1.38

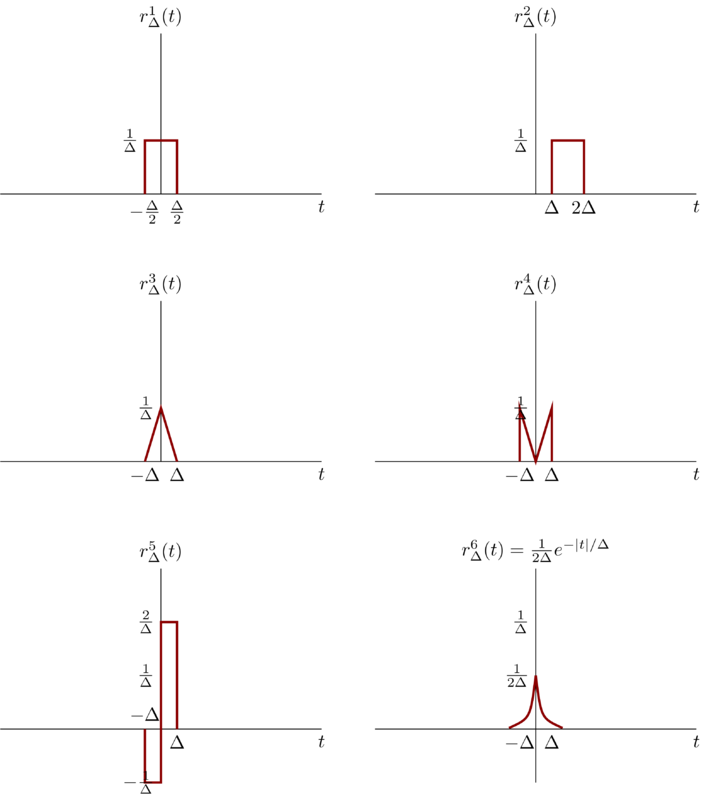
Problem 1.38a

Base on fig 1 , \(\delta(2t)\) can be visualized as follows

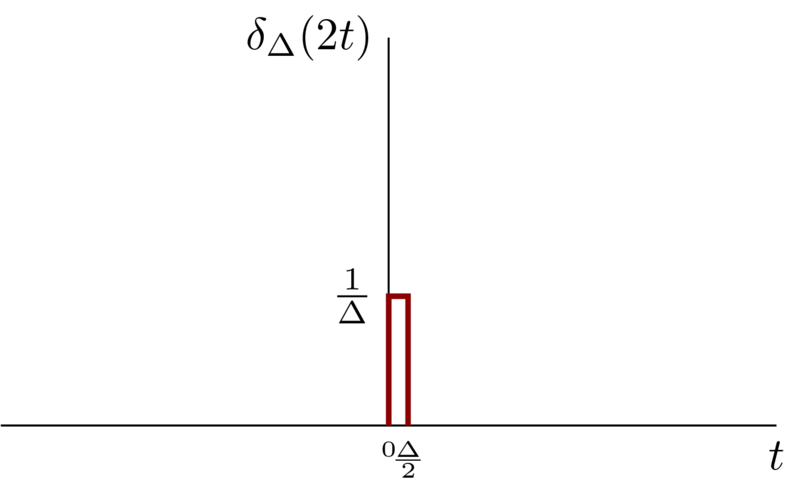
Based on the fact \(\delta(t)\) has unit area, so \(\delta(2t)\) will have \(\frac{1}{2}\) . So \(\delta(2t) = \frac{1}{2}\delta(t)\).

Problem 1.38b

Because

\begin{equation*} u_{\Delta}(t) = \int_{-\infty}^{t}\delta_{\Delta}(\tau)d\tau \end{equation*}

We can get \(u_{\Delta}^{1}(t)\) easily.

\(r_{\Delta}^{1}(t)\) can be represented as

\begin{equation*} r_{\Delta}^{1}(t) = \begin{cases} \frac{1}{\Delta}, & -\frac{\Delta}{2} \leq t \leq \frac{\Delta}{2} \\
0, & \mathrm{Otherwise} \end{cases} \end{equation*}

Then during the integration, \(u_{\Delta}^{1}(t)\) can be represented as

\begin{equation*} u_{\Delta}^{1}(t) = \begin{cases} 0, & t < -\frac{\Delta}{2} \\
\frac{t}{\Delta}, & -\frac{\Delta}{2} \leq t \leq \frac{\Delta}{2} \\
1, & t > \frac{\Delta}{2} \end{cases}

\end{equation*}

we can express the \(r_{\Delta}^{2}(t)\) as :

\begin{equation*} r_{\Delta}^{2}(t) = \begin{cases} \frac{1}{\Delta} , & \Delta \leq t \leq 2\Delta \\
0, & \mathrm{Otherwise} \end{cases} \end{equation*}

So the \(u_{\Delta}^{2}(t)\) can be expressed as:

\begin{equation*} u_{\Delta}^{2}(t) = \begin{cases} 0, & t < \Delta \\
\frac{t-\Delta}{\Delta} & \Delta \leq t \leq 2\Delta \\
1, & t> 2\Delta \end{cases} \end{equation*}

We express \(r_{\Delta}^{3}(t)\) as:

\begin{equation*} r_{\Delta}^{3}(t) = \begin{cases} \frac{1}{\Delta^{2}} ( t + \Delta) , & - \Delta < t \leq 0 \\
\frac{1}{\Delta^{2}} ( -t + \Delta) , & 0 < t \leq \Delta \\
0, & \mathrm{otherwise} \end{cases} \end{equation*}

and \(u_{\Delta}^{3}(t)\):

\begin{equation*} u_{\Delta}^{3}(t) = \begin{cases} \frac{1}{\Delta^{2}}( \frac{t^{2}}{2} + \Delta t + \frac{\Delta^{2}}{2}) ,& -\Delta < t \leq 0 \\
\frac{1}{2} + \frac{1}{\Delta^{2}} ( - \frac{t^{2}}{2} + \Delta t ) , & 0 < t < \Delta \\
1, & t > \Delta \end{cases} \end{equation*}

So we can visualize them as follows:

We can represent \(r_{\Delta}^{4}(t)\) as :

\begin{equation*} r_{\Delta}^{4}(t) = \begin{cases} - \frac{1}{\Delta^{2}} t , & -\Delta < t \leq 0 \\
\frac{1}{\Delta^{2}} t , & 0 < t \leq \Delta \\
0, & \mathrm{Otherwise} \end{cases} \end{equation*}

and \(u_{\Delta}^{4}(t)\)

\begin{equation*} u_{\Delta}^{4}(t) = \begin{cases} 0, & t < -\Delta \\
- \frac{t^{2}}{2\Delta^{2}} + \frac{1}{2}, & - \Delta < t \leq 0\\
\frac{t^{2}}{2\Delta^{2}} + \frac{1}{2}, & - \Delta < t \leq 0\\
1, & t > \Delta \end{cases} \end{equation*}

and we visualize them as:

We can express \(r_{\Delta}^{5}(t)\) as :

\begin{equation*} r_{\Delta}^{5}(t) = \begin{cases} - \frac{1}{\Delta} , & -\Delta < t \leq 0 \\
\frac{2}{\Delta} , & 0 < t \leq \Delta \\
0, & \mathrm{Otherwise} \end{cases} \end{equation*}

and \(u_{\Delta}^{5}(t)\) as:

\begin{equation*} u_{\Delta}^{5}(t) = \begin{cases} - \frac{t}{\Delta} -1, & -\Delta < t < 0 \\
-1 + \frac{2t}{\Delta} , & 0 < t \leq \Delta \\
1,& t > \Delta \end{cases} \end{equation*}

So we can visualize them as below:

We can express \(r_{\Delta}^{6}(t)\) as :

\begin{equation*} r_{\Delta}^{6}(t) = \frac{1}{2\Delta} e^{-|t|/\Delta} \end{equation*}

and \(u_{\Delta}^{6}(t)\) as :

\begin{equation*} u_{\Delta}^{6}(t) = \begin{cases} \frac{1}{2} e^{\frac{t}{\Delta}} , & t< 0 \\
1 - \frac{1}{2}e^{ \frac{-t}{\Delta}} , & t> 0 \\
\end{cases} \end{equation*}

So we can visualize them as below:

8 Problem 1.39

\begin{equation*} \lim_{\Delta\to 0} [u_{\Delta}(t)\delta(t)] = \lim_{\Delta\to 0} [u_{\Delta}(t)\delta(0)] = 0 \end{equation*}

And

\begin{eqnarray*} \lim_{\Delta\to 0} [u_{\Delta}(t)\delta_{\Delta}(t)] &=& \lim_{\Delta\to 0 } \frac{1}{2} \frac{d u_{\Delta}^{2}(t)}{dt} \\
&=& \frac{1}{2} \delta(t) \end{eqnarray*}

Notice that when \(\Delta\to 0\) the item \( \frac{u_{\Delta}^{2}(t)}{dt} \) also approach to \(\delta(t)\).

for equation:

\begin{equation*} g(t) = \int_{-\infty}^{+\infty} u( \tau )\delta(t-\tau)d\tau \end{equation*}

we have

\begin{equation*} g(t) = \begin{cases} 0, & t< 0 \\
1, & t> 0 \\
\mathrm{undefined}, & t = 0 \end{cases}

\end{equation*}

So \(g(t)\) has the same property as \(u(t)\)

9 Problem 1.40

Problem 1.40a

Problem 1.40b

It is easy to construct such a system, for a continuous-time version, we have \(y(t) = x^{2}(t)\) and it discrete-time counterparts \(y[n] = x^{2}[n]\)

We cannot reach that conclusion. Because for a system has memory, a certain zero period \(t_{1}\) to \(t_{2}\) does not result the same zero period in the output. Let’s take \(y[n] = x[n-n_{0}]\) where \(n_{0}\neq 0\), the output will have a delay ( \(n_{0}\) is positive) and an advance ( \(n_{0}\) is negative).

10 Problem 1.41

Problem 1.41a

If \(g[n] = 1 \forall \ n\) , then we have

\begin{equation*} y[n] = 2x[n] \end{equation*}

Next, we proof that this system is time invariant. Let \(x_{1}[n]\) and \(y_{1}[n]\) are the input and output respectively i.e.

\begin{equation*} y_{1}[n] = 2x_{1}[n] \end{equation*}

Let \(x_{2}[n] = x_{1}[n-n_{0}]\) then we have

\begin{equation*} y_{2}[n] = 2x_{2}[n] = 2x_{1}[n-n_{0}] = 2y_{1}[n-n_{0}] \end{equation*}

So we have that one time shift in the input signal will result in an identical time shift in the output. The system is time invariant.

if \(g[n] = n\), we have

\begin{equation*} y[n] = (2n-1) x[n] \end{equation*}

Let \(x_{1}[n]\) and \(y_{1}[n]\) the input and output respectively, i.e.

\begin{equation*} y_{1}[n] = (2n-1)x_{1}[n] \end{equation*}

Let \(x_{2}[n] = x_{1}[n-n_{0}]\), then we have

\begin{equation*} y_{2}[n] = (2n-1)x_{2}[n] = (2n-1)x_{1}[n-n_{0}] \end{equation*}

We also have:

\begin{equation*} y_{1}[n-n_{0}] = ( 2(n-n_{0}) ) x_{1}[n-n_{0}] \end{equation*}

Obviously, \(y_{2}[n]\neq y_{1}[n-n_{0}]\). The system is time invariant.

If \(g[n] = 1 + (-1)^{n}\), then

\begin{equation*} g[n] + g[n-1] = 1 + (-1)^{n} + 1 + (-1)^{n-1} = 2 \end{equation*}

Which means that the system is identical as the system in part (a) and hence the system is time invariant.

11 Problem 1.42

Let \(\mathcal{S}_{1}\) and \(\mathcal{S}_{2}\) two connected LTI system. Let \(x_{11}(t)\) and \(x_{12}(t)\) arbitrary signals, \(a_{1}\) and \(b_{1}\) arbitrary consstants.

Then:

\begin{eqnarray*} x_{11}(t)&\xrightarrow{\mathcal{S}_{1}} & y_{11}(t) \\
x_{12}(t)&\xrightarrow{\mathcal{S}_{1}} & y_{12}(t) \\
\end{eqnarray*}

Let \(x_{13}(t) = a_{1} x_{11}(t) + b_{1}x_{12}(t)\), then

\begin{equation*} x_{13}(t) = a_{1} x_{11}(t) + b_{1}x_{12}(t) \xrightarrow{\mathcal{S}_{1}} y_{13}(t) = a_{1}y_{11}(t) + b_{1} y_{12}(t) \end{equation*}

For System \(\mathcal{S}_{2}\), we have the similar results:

\begin{eqnarray*} x_{21}(t)&\xrightarrow{\mathcal{S}_{2}} & y_{21}(t) \\
x_{22}(t)&\xrightarrow{\mathcal{S}_{2}} & y_{22}(t) \\
\end{eqnarray*}

Let \(x_{23}(t) = a_{2} x_{21}(t) + b_{2}x_{22}(t)\), then

\begin{equation*} x_{23}(t) = a_{2} x_{21}(t) + b_{2}x_{22}(t) \xrightarrow{\mathcal{S}_{2}} y_{23}(t) = a_{2}y_{21}(t) + b_{2} y_{22}(t) \end{equation*}

Because \(S_{1}\) and \(S_{2}\) are interconnected in series. So let \( x_{21}(t) = y_{11}(t) \) and \(x_{22}(t) = y_{12}(t)\) we can see the overall system is linear.

Next we check the time invariant property of the overall system. Since \(\mathcal{S}_{1}\) and \(S_{2}\) are time invariant. we have

\begin{eqnarray*} x_{1}(t-t_{1})&\xrightarrow{\mathcal{S}_{1}}& y_{1}(t-t_{1}) \\
x_{2}(t-t_{2})&\xrightarrow{\mathcal{S}_{2}}& y_{2}(t-t_{2}) \end{eqnarray*}

Since the two systems are in series, the overall system is time invariant.

False, we just take one counterexample. Consider the following two nonlinear systems.

\begin{eqnarray*} y_{1}[n] &=& x_{1}[n] + 1 \\
y_{2}[n] &=& x_{2}[n] - 1 \end{eqnarray*}

Since the two systems are in series. Let \(y_{1}[n] = x_{2}[n]\), then we have the overall system \(y_{2}[n] = x_{1}[n]\) which is linear.

First we can express the interconnection of system 1 and system 2 as:

\begin{equation*} y[n] = \begin{cases} x[ \frac{n}{2} ] + \frac{1}{4} x[ \frac{n-2}{2} ] , & n \ \mathrm{even} \\
\frac{1}{2} x[ \frac{n-1}{2} ] , & n \ \mathrm{odd} \end{cases} \end{equation*}

Then we express the interconnection of all the three systems.

\begin{equation*} y[n] = x[ \tfrac{2n}{2} ] + \tfrac{1}{4} x[ \tfrac{2n-2}{2} ] = x[n] + \tfrac{1}{4} x[n-1] \end{equation*}

So the system is an LTI system.

12 Problem 1.43

Problem 1.43a

For a time-invariant system, an arbitrary time shifting \(t_{0}\) in the input will result in an identical time shifting in the output. So let the \(t_{0}\) be the period \(T\), the the output should also be a time shifting \(T\). Because the system is period \(x(t) = x(t+T)\), then the output \(y(t) = y(t+T)\).

For the descrete time, the conclusion also holds.

Suppose that we have a system:

\begin{equation*} y[n] = 1 \end{equation*}

Then this system is time-invariant, any input will not change the property of its output.

13 Problem 1.44

Problem 1.44a

A system is causal if the output at any time depends on values of the input at only the present and past times.

Let’s suppose that \(y(t) \neq 0, t< t_{0} \), which mean for some \(x(t) \neq 0, t< t_{0}\). However this is not true. So for \(x(t) = 0, t< t_{0}\), it must be that \(y(t)= 0 , t< t_{0}\)

\(y(t) = x^{2}(t)x^{2}(t+1)\) where \(x(t) = 0, t< t_{0}\).

\(y(t) = x(t) + 1\)

First let’s proof that suppose \(y[n] = 0, \forall n\) if \(x[n]=0 ,\forall n\) , then the system is invertible.

let \(x_{1}[n]\) and \(x_{2}[n]\) be two arbitrary inputs and these two inputs lead to the same output \(y_{1}[n]\) .

\begin{eqnarray*} x_{1}[n] &\xrightarrow{\mathcal{S}}& y_{1}[n] \\
x_{2}[n] &\xrightarrow{\mathcal{S}}& y_{1}[n] \end{eqnarray*}

Because the system is linear.

\begin{equation*} x_{1}[n] - x_{2}[n] \xrightarrow{\mathcal{S}} y_{1}[n]-y_{1}[n] = 0 \end{equation*}

So we must have \(x_{1}[n] = x_{2}[n]\) which is not consist with the assumption and means that any output \(y_{1}[n]\) must have single one input. i.e. the system is invertible.

Next we proof that for a invertible linear system, \(y[n] = 0, \forall n \) if and only if \(x[n] = 0, \forall n\)

If \(x[n] = 0\), then we have

\begin{eqnarray*} x[n] = 0 &\xrightarrow{\mathcal{S}} &y[n] \\
\alpha x[n] = 0 &\xrightarrow{\mathcal{S}}& \alpha y[n] \end{eqnarray*}

where \(\alpha\) is arbitrary constants. Because the system is invertible, so the same input \(0\) must lead to the same output, so \(y[n]=\alpha y[n] \). then \(y[n] = 0\).

\(y[n] = x^{m}[n] , m\neq 1 \ \mathrm{and}\ m\neq 0 \)

\(m=1\) \(y[n] = x[n]\) is a linear system. \(m=0\), \(y[n] = 1\) does satisfies that \(y[n]= 0, \forall n\)

14 Problem 1.45

First, let’s recall the definition of \(\phi_{hx}(t)\):

\begin{equation*} \phi_{hx}(t) = \int_{-\infty}^{+\infty} h(t + \tau)x(\tau)d\tau \end{equation*}

Problem 1.37a

Let \(x_{1}(t)\) and \(x_{2}(t)\) two arbitrary input signals, and \(\alpha\) and \(\beta\) two arbitrary constants. Let \(x_{3}(t) = \alpha x_{1}(t) + \beta x_{2}(t) \), then we have

\begin{eqnarray*} \phi_{hx_{1}}(t) &=& \int_{-\infty}^{+\infty} h(t+\tau)x_{1}(\tau)d\tau \\
\phi_{hx_{2}}(t) &=& \int_{-\infty}^{+\infty} h(t+\tau)x_{2}(\tau)d\tau \\
\phi_{hx_{3}}(t) &=& \int_{-\infty}^{+\infty} h(t+\tau)x_{3}(\tau)d\tau \\
&=& \int_{-\infty}^{+\infty} h(t+\tau)( \alpha x_{1}(t) + \beta x_{2}(t) )d\tau \\
&=& \alpha \int_{-\infty}^{+\infty} h(t+\tau)x_{1}(\tau)d\tau + \beta \int_{-\infty}^{+\infty} h(t+\tau)x_{2}(\tau)d\tau \\
&=& \alpha \phi_{hx_{1}}(t) + \beta \phi_{hx_{2}}(t) \end{eqnarray*}

Then we have that the system is linear.

Next we check the property of time invariance.

Let \(x_{4}(t) = x_{1}(t+T_{0})\) So

\begin{eqnarray*} \phi_{hx_{4}}(t) &=& \int_{-\infty}^{+\infty} h(t+\tau)x_{4}(\tau)d\tau \\
&=& \int_{-\infty}^{+\infty} h(t+\tau)x_{1}(\tau + T_{0})d\tau \\
&=& \int_{-\infty}^{+\infty} h(t+s-T_{0})x_{1}(s)ds \\
&=& \phi_{hx_{1}}(t-T_{0}) \end{eqnarray*}

We have \(\phi_{hx_{4}}(t)\neq \phi_{hx_{1}}(t+T_{0})\). So the system is not time invariant.

The system is not causal, because the output depends on all time of the input.

\(\phi_{xh}(t)\) can be expressed as

\begin{equation*} \phi_{xh}(t) = \int_{-\infty}^{+\infty} x(t+ \tau) h(\tau)d\tau \end{equation*}

Based on similar analysis as in part (a), we can conclude that the system is linear.

Next, we check the property of time invariance. Let \(x_{1}(t)\) be arbitrary input signal and \(x_{4}(t) = x_{1}(t+T_{0})\) then we have

\begin{eqnarray*} \phi_{x_{4}h}(t) &=& \int_{-\infty}^{+\infty} x_{4}(t+\tau) h(\tau) d\tau \\
&=& \int_{-\infty}^{+\infty} x_{1}(t+T_{0}+\tau) h(\tau) d\tau \\
&=& \phi_{x_{1}h}(t+T_{0}) = \phi_{x_{1}h}(t+T_{0}) \end{eqnarray*}

Which means that the system is time invariant.

The system is not causal because the output depends on all the value of \(x(t)\).

15 Problem 1.46

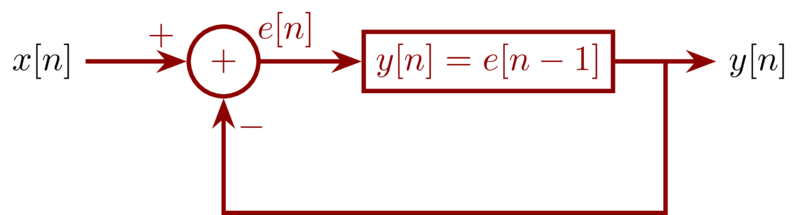
From the figure given, we have:

\begin{eqnarray*} e[n]&=& x[n] - y[n] \\
y[n] &=& e[n-1] \end{eqnarray*}

So we have \(y[n] = x[n-1] - y[n-1]\)

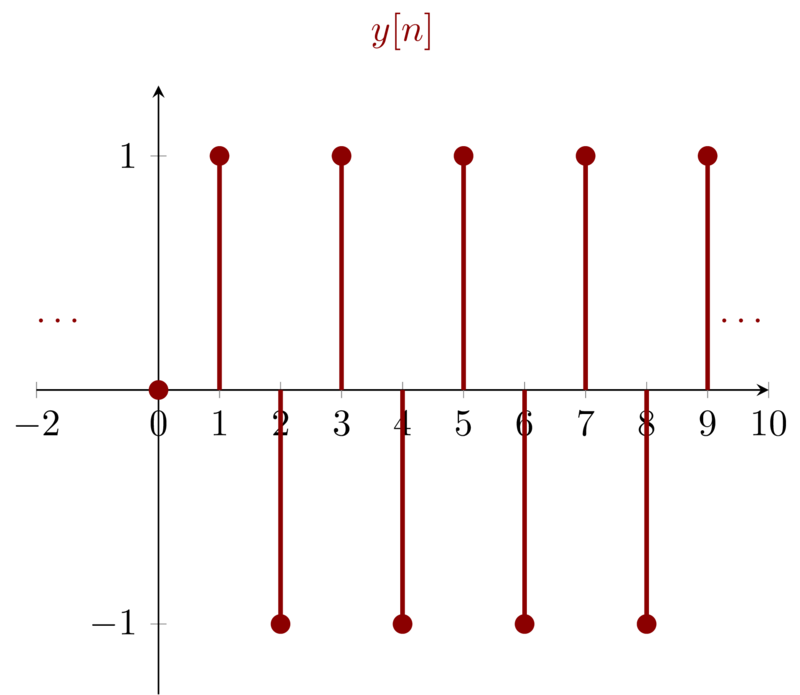
Problem 1.46a

\(x[n] = \sigma[n]\) So we have \(x[0] = 1\) and \(x[n] = 0, n\neq 0\)

\begin{eqnarray*} y[0]&=& x[-1] - y[-1] = 0 \\
y[1]&=& x[0] - y[0] = 1 \\
y[2]&=& x[1] - y[1] = -1 \\
y[3]&=& x[2] - y[2] = 1 \\
\end{eqnarray*}

So the output can be sketched as:

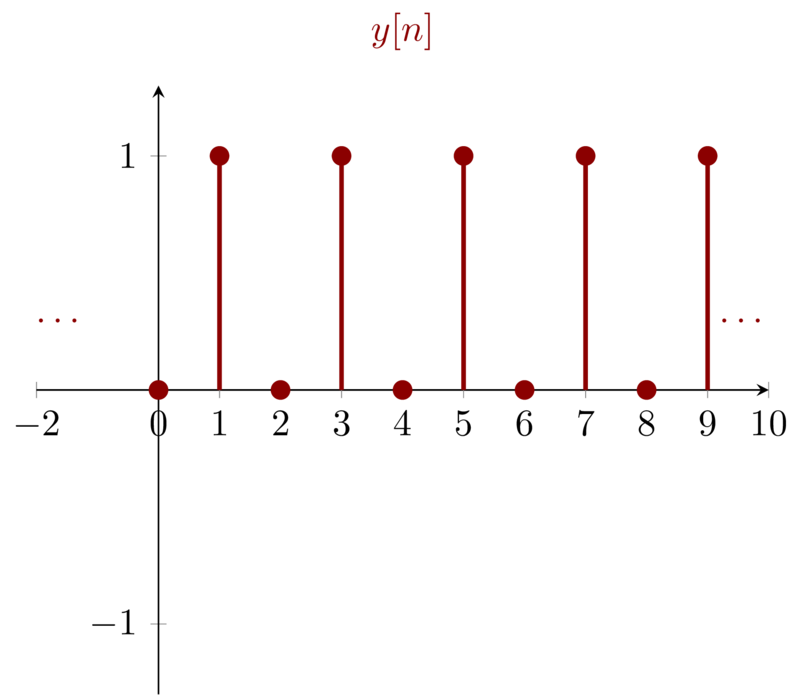
Problem 1.46b

\(x[n] = u[n]\) So we have \(x[n] = 1, n\geq 0\)

\begin{eqnarray*} y[0]&=& x[-1] - y[-1] = 0 \\
y[1]&=& x[0] - y[0] = 1 \\
y[2]&=& x[1] - y[1] = 0 \\
y[3]&=& x[2] - y[2] = 1 \\
\end{eqnarray*}

So the output can be sketched as:

16 Problem 1.47

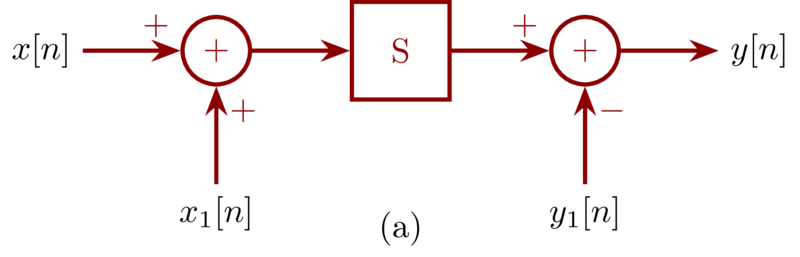
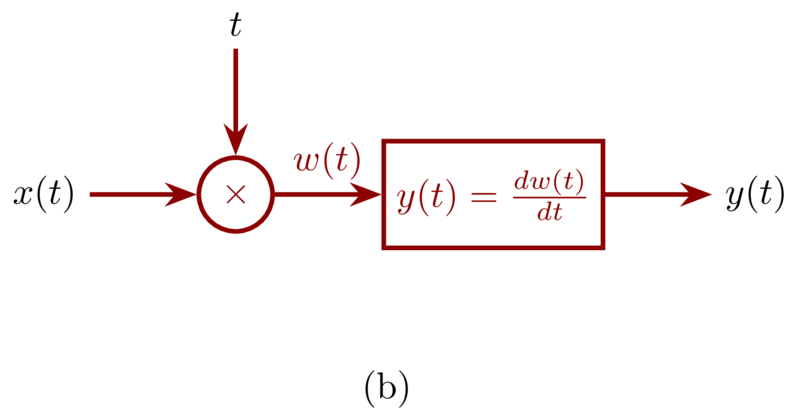
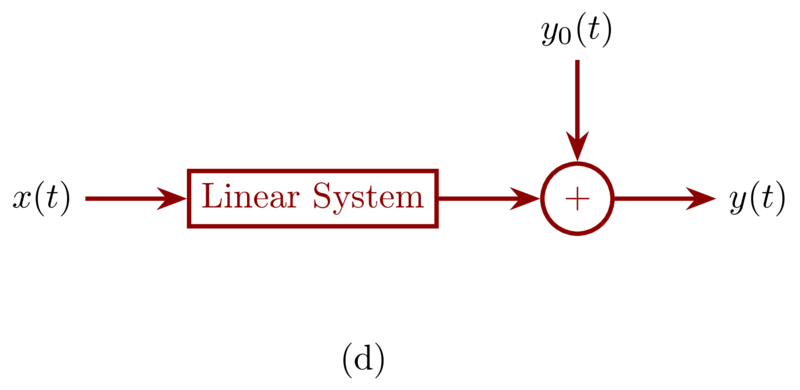
Problem 1.47a

An incrementally linear system can be expressed as Figure 1-47d : a linear system followed by another signal equal to the zero-input response of the system. Because \(\mathcal{S}\) is an incrementally linear system, the output \(y[n] = y^{‘}[n] - y_{1}[n]\) where \(y^{‘}[n]\) is the output of \(\mathcal{S}\). The \(y^{‘}[n]\) contains the response of \(x[n]\) and \(x_{1}[n]\) i.e. \(y^{‘}[n]\) at lease contains \(y_{1}[n]\). So \(y[n] = y^{‘}[n] - y_{1}[n]\) will not containt the zero-input response of system \(\mathcal{S}\). and the overall system from \(x[n]\) to \(y[n]\) only have the result of the linear part of system \(\mathcal{S}\) hence the system is linear.

Furthermore, no matter what \(x_{1}[n]\) we choose, its effect will be cancelled by substracting \(y_{1}[n]\). hence, the overall input-output relationship between \(x[n]\) and \(y[n]\) does not depend on the particular choice of \(x_{1}[n]\).

Problem 1.47b

\(\mathcal{S}\) is an incrementally linear system. By substracting its zero-input response \(y_{0}[n]\) we have a linear system.

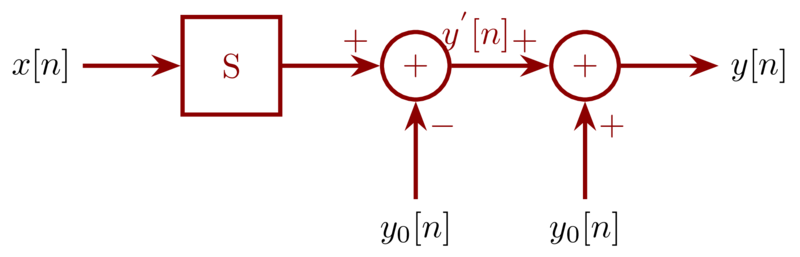
The system from \(x[n]\) to \(y^{‘}[n]\) is the linear part, and the overall input-output is the system \(\mathcal{S}\) represented as incrementally linear system.

Problem 1.47c-1

The system is incrementally linear with the linear part:

\begin{equation*} x[n] \xrightarrow{\mathcal{L}} x[n] + 2x[n+4] \end{equation*}

and the zero-input response

\begin{equation*} y_{0}[n] = n \end{equation*}

Problem 1.47c-2

The system is incrementally linear with the linear part:

\begin{equation*} x[n] \xrightarrow{\mathcal{L}} \begin{cases} 0, & n\ \mathrm{even} \\
\sum_{k=-\infty}^{(n-1)/2}x[k], & n\ \mathrm{odd} \end{cases} \end{equation*}

and the zero-input response

\begin{equation*} y_{0}[n] = \begin{cases} n/2 , & n\ \mathrm{even} \\
(n-1)/2, & n\ \mathrm{odd} \end{cases} \end{equation*}

Problem 1.47c-3

Not incrementally linear system. because for \(x[0] \geq 0\) there is one zero-input response \(+3\), for \(x[0] < 0\), there is one zero-input response \(-3\). So the overall system cannot choose one zero-input response.

Problem 1.47c-4

The overall system can be expressed as

\begin{equation*} y(t) = x(t) + t\frac{dx(t)}{t} \end{equation*}

The system is linear itself and of course is incrementally linear with zero-input reponse zero.

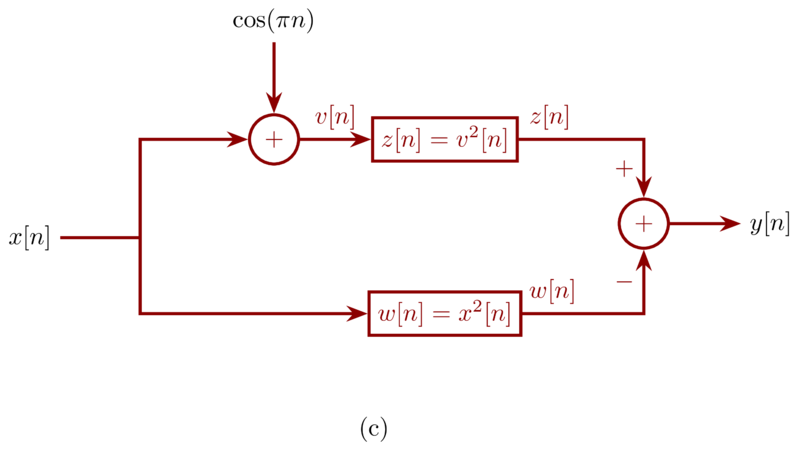
Problem 1.47c-5

The overall system can be expressed as:

\begin{eqnarray*} y[n]&=& (x[n] + \cos(\pi n))^{2} - (x^{2}[n]) \\
&=& 2x[n]\cos(\pi n) + \cos^{2}(\pi n) \end{eqnarray*}

Therefore, the system is incrementally linear with the linear part:

\begin{equation*} x[n] \xrightarrow{\mathcal{L}} 2x[n]\cos(\pi n) \end{equation*}

and the zero-input response

\begin{equation*} y_{0}[n] = \cos^{2}(\pi n) \end{equation*}

Problem 1.47d

First, let’s proof that if \(\mathcal{S}\) is time invariant we can conclude that \(\mathcal{L}\) is a time-invariant system and \(y_{0}[n]\) is constant

For the linear part we have:

\begin{equation*} x[n] \xrightarrow{\mathcal{L}} L[n] \end{equation*}

And the zero-input part.

\begin{equation*} y[n] = L[n] + y_{0}[n] \end{equation*}

Suppose \(\mathcal{S}\) is time invariant, let \(x_{1}[n]\) and arbitrary input signal.

\begin{equation*} y_{1}[n] = x_{1}[n] + y_{0}[n] \end{equation*}

and let \(x_{2}[n]\) be \(x_{1}[n-n_{0}]\), where \(n_{0}\) is an arbitrary integer So

\begin{equation*} y_{2}[n] = x_{2}[n] + y_{0}[n] = x_{1}[n-n_{0}] + y_{0}[n] \end{equation*}

we also have \(y_{1}[n-n_{0}] = x_{1}[n-n_{0}] + y_{0}[n-n_{0}]\) and \(y_{2}[n] = y_{1}[n-n_{0}]\), so we have \(y_{0}[n] = y_{0}[n-n_{0}]\). Since \(n_{0}\) is an arbitrary integer, so \(y_{0}[n]\) must be an constant.

Also \(y_{2}[n] = y_{1}[n-n_{0}]\) also implies that \(L_{1}(n-n_{0}) = L_{2}[n]\) which means that the linear part is time invariant.

Next, let’s proof that if \(\mathcal{L}\) is a time-invariant system and \(y_{0}[n]\) is constant then \(\mathcal{S}\) is time invariant. This is easy to reach when we write \(\mathcal{S}\) as linear part plus and the zero-input consponse:

For the linear part we have:

\begin{equation*} x[n] \xrightarrow{\mathcal{L}} L[n] \end{equation*}

And the zero-input part.

\begin{equation*} y[n] = L[n] + y_{0}[n] \end{equation*}

\(\mathcal{L}\) is time-invariant means that \(L[n]\) will experience the same time shifting as \(x[n]\) will be. \(y_{0}[n]\) is constant means that \(y_{0}[n]\) will not change as time shifts. So \(\mathcal{S}\) is time-invariant.